Calcular el área de un triángulo puede parecer complicado al principio, pero todo es difícil al principio ¿no? Aquí te vamos a enseñar paso a paso qué es el área, cómo se calcula, diferentes fórmulas y cómo resolver ejercicios prácticos, dependiendo del tipo de triángulo.
¿Qué es el área de un triángulo?
El área de un triángulo es la medida de la superficie que ocupa. En otras palabras, es “el espacio que hay dentro” del triángulo. Se expresa normalmente en unidades cuadradas (cm², m², etc.).
Saber cómo se calcula el área es importante para:
- Resolver problemas de geometría.
- Medir terrenos o superficies.
- Entender fórmulas matemáticas más complejas.
¿Cómo se calcula el área de un triángulo?
La fórmula más común para hallar el área es:
Área = (base × altura) ÷ 2
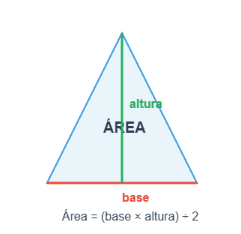
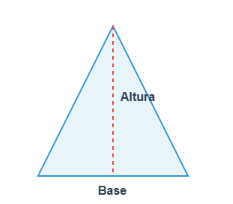
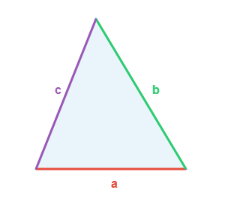
Esta fórmula se aplica cuando conocemos la base y la altura del triángulo. Recuerda que la altura es la línea recta (verde en la imagen) que va desde un vértice hasta el lado opuesto (o su prolongación), formando un ángulo recto. La base es la de abajo (roja)
Cálculo según el tipo de triángulo
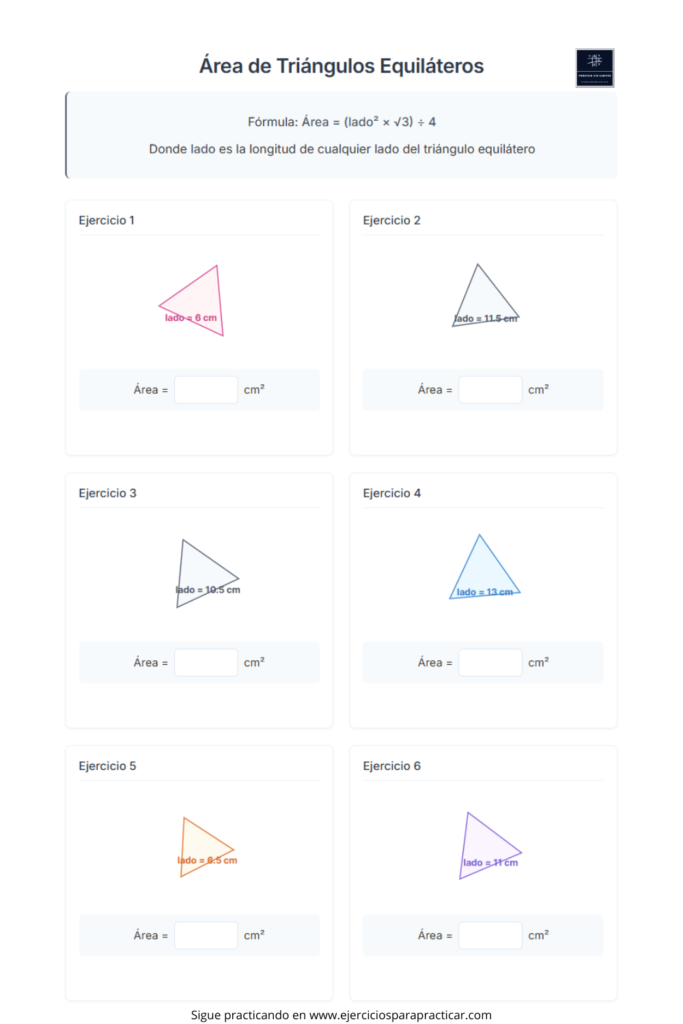
Área de un triángulo equilátero
Todos sus lados son iguales y todos hacen un ángulo de 60º. Se puede calcular con esta fórmula:
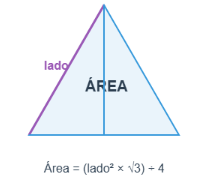
Área = (lado² × √3) ÷ 4
Área de un triángulo isósceles
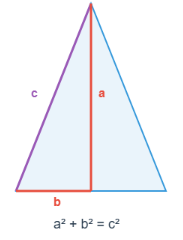
Tiene dos lados iguales. Si conoces la base y la altura, aplica la fórmula estándar. Si solo tienes los lados, puedes usar trigonometría o el Teorema de Pitágoras.
Área de un triángulo escaleno
Todos los lados son diferentes. Aquí no puedes usar base × altura directamente si no conoces la altura. En ese caso, aplica la fórmula de Herón:
Herón:
s = (a + b + c) ÷ 2
Área = √[s(s−a)(s−b)(s−c)]
Área de un triángulo rectángulo
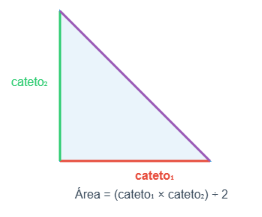
Uno de sus ángulos mide 90°. La fórmula estándar sirve perfectamente:
Área = (cateto1 × cateto2) ÷ 2
Otras formas de calcular el área
✅ Usando trigonometría (cuando conoces dos lados y el ángulo entre ellos)
Área = (a × b × sen(θ)) ÷ 2

✅ Con coordenadas (ideal para geometría analítica)
Fórmulas especiales que se aplican en el plano cartesiano usando puntos (x, y).
Ejemplos y ejercicios resueltos
Veamos cómo se aplican estas fórmulas con ejemplos paso a paso.
🧩 Ejemplo 1:
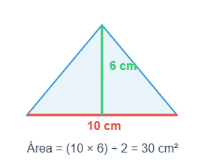
Un triángulo tiene base 10 cm y altura 6 cm.
Área = (10 × 6) ÷ 2 = 30 cm²
🧩 Ejemplo 2:
Un triángulo equilátero de lado 8 cm.
Área = (8² × √3) ÷ 4 ≈ 27.71 cm²

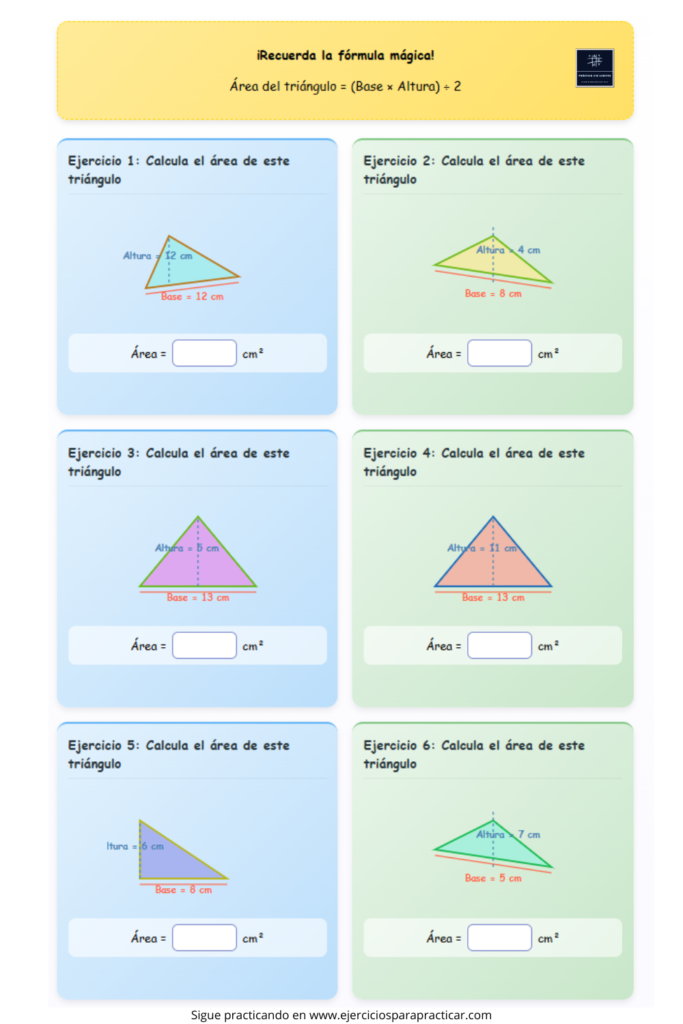
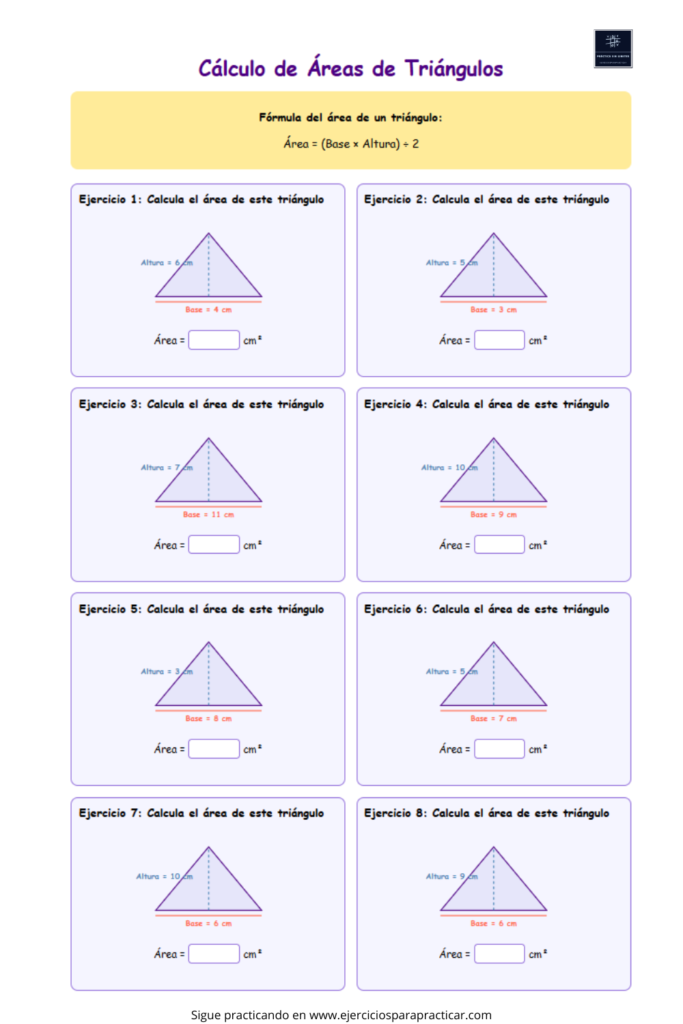
Ejercicios para practicar (fichas imprimibles)
Aquí tienes fichas para trabajar el área de triángulos en casa o en clase:
Errores comunes al calcular el área
Evita estos errores típicos:
- Confundir la base con el lado más largo.
- No usar la altura perpendicular real.
- Usar fórmulas que no aplican al tipo de triángulo.
- Olvidar dividir entre 2 en la fórmula estándar.
💡 Consejo: dibuja el triángulo y marca base y altura antes de empezar.
Trucos para recordar la fórmula
- Imagínate que el triángulo es la mitad de un rectángulo.
- Asocia la palabra "base" con "bajo", lo que está abajo.
- Usa esta rima:
“Multiplica base con altura,
luego divide entre dos con soltura.”
Accede a nuestra página para descubrir mas fichas educativas y mas ejercicios para que puedas practicar.