Los números están presentes en cada aspecto de nuestra vida: desde contar dinero hastacontar las paradas de bus que nos faltan hasta llegar a nuestro destino. Sin embargo, pocas veces nos detenemos a pensar en qué es un sistema de numeración y cómo ha evolucionado a lo largo de la historia.
Los sistemas de numeración han sido desarrollados por diferentes civilizaciones con el propósito de representar cantidades de manera eficiente. Actualmente, utilizamos el sistema decimal, pero en el pasado existieron otros sistemas igualmente importantes y lo vamos a ir viendo en este artículo.
¿Cuál es nuestro sistema numérico?
Empecemos por lo que tenemos mas cerca, el ahora, cuando hablamos de nuestro sistema de numeración actual, nos referimos al sistema decimal o de base 10. Este sistema se basa en diez dígitos (0-9) y es de tipo posicional, lo que significa que la posición de cada número determina su valor. Esto no significa que solo podamos contar hasta el 10, esto significa que esto son los números que hay y de alli los combinamos para que vayan sumando y representando cantidades.
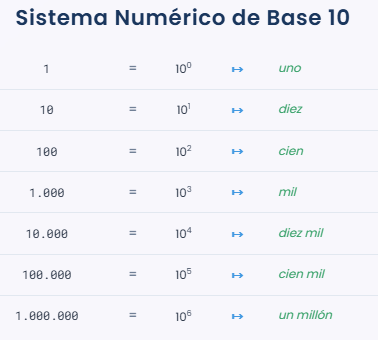
¿Por qué usamos el sistema decimal?
El sistema decimal es el más utilizado en todo el mundo debido a su facilidad de uso y a que probablemente se desarrolló por la costumbre de contar con los diez dedos de las manos. Además a la hora de enseñar a los niños los números, se vuelve mucho mas fácil.
Sin embargo, en matemáticas e informática, se utilizan otros sistemas, como el binario (base 2) en informática, el octal (base 8) en ciertas aplicaciones electrónicas y el hexadecimal (base 16) en programación.
Comparación con otros sistemas númericos
| Sistema de numeración | Base | Ejemplo de representación del número 10 |
|---|---|---|
| Decimal | 10 | 10 |
| Binario | 2 | 1010 |
| Octal | 8 | 12 |
| Hexadecimal | 16 | A |
Nuestro sistema decimal es eficiente para nosotros, pero no es el único que se usa hoy en día, pero como puedes ver en la tabla de arriba, el que nos resulta mas fácil es el sistema decimal, ya que es el que estamos acostumbrados. Seguramente si nos dijerán de contar en sistema binario, la mayoria tardaríamos horas en decir el número que queremos.
Propiedades y diferencias de los sistemas de numeración
Cada sistema de numeración tiene ciertas propiedades que lo distinguen:
- Base numérica: Es el número de símbolos utilizados en el sistema (ejemplo: base 10 en el decimal, base 2 en el binario).
- Posicionalidad: Algunos sistemas consideran la posición del dígito para determinar su valor, como el decimal, mientras que otros, como el romano, no son posicionales.
- Símbolos o cifras: Los sistemas pueden usar números (0-9 en decimal) o letras y otros caracteres, como en el sistema hexadecimal.
Sistemas de numeración antiguos
Antes de que el sistema decimal se convirtiera en el estándar mundial y lo empezamos a utilizar, muchas civilizaciones desarrollaron sus propios métodos de numeración.
Algunos sistemas de numeración antiguos
- Sistema de numeración egipcio: Utilizaba jeroglíficos y no era posicional.
- Sistema babilónico: Basado en la base 60, influyó en la medición del tiempo (60 segundos, 60 minutos).
- Sistema maya: Usaba base 20 y un concepto temprano del número cero.
- Sistema de numeración griego: utilizaba letras del alfabeto para representar números. Era similar al sistema romano, ya que no era posicional y se basaba en símbolos.
Estos sistemas sentaron las bases para el desarrollo de los sistemas modernos que usamos hoy en día. Pero lo interesante era que cada uno de estos sistema de numeración utilizaron y desarrollaron sus propios estudios científicos con otro tipo de números, para asi decirlo.
Sistemas de numeración posicional
Uno de los avances más importantes en la historia de la numeración fue el desarrollo de los sistemas de numeración posicional. En estos sistemas, el valor de un número depende de la posición que ocupa cada dígito dentro de la cifra.
¿Qué es un sistema de numeración posicional?
Un sistema de numeración posicional utiliza un conjunto de símbolos y una base determinada para representar cantidades. En este tipo de sistema, cada posición tiene un valor diferente y se multiplica por una potencia de la base. Como por ejemplo en los ejercicios de números romanos que solemos utilizar en matemáticas.
Diferencias entre sistemas posicionales y no posicionales
| Característica | Sistemas posicionales | Sistemas no posicionales |
|---|---|---|
| Valor depende de la posición | Sí | No |
| Base numérica definida | Sí | No necesariamente |
| Ejemplos | Decimal, binario, octal | Romano, egipcio |
Base de un sistema de numeración
¿Qué es la base de un sistema de numeración?
La base de un sistema de numeración es el número total de símbolos distintos utilizados para representar valores en ese sistema.

Importancia de la base numérica en informática y matemáticas
En matemáticas, la base numérica define la manera en que representamos los números y realizamos operaciones, también se utiliza en física para dar una explicación a todo lo que pasa a nuestro alrededor. En informática, los sistemas binario, octal y hexadecimal son esenciales para la codificación de datos, programación y diseño de hardware.
Por ejemplo, los colores en HTML se representan en hexadecimal:
- #FF0000 representa el color rojo.
- #00FF00 representa el color verde.
- #0000FF representa el color azul.
Entender estas bases númericas es muy necesario en algunas disciplinas, ya que si no fuera por estos, nada tendría sentido o sería un caos. Aúnque a veces es complicado saberse, por ejemplo, todos los colores en el sistema hexadecimal, por eso existen programas especiales para saber que "código" representa cada color.
Propiedades de los sistemas de numeración
Cada sistema de numeración tiene características únicas que lo diferencian de otros.
Principales propiedades de los sistemas numéricos
- Unicidad: Cada número tiene una única representación dentro de su sistema.
- Base fija: Define la cantidad de símbolos utilizados.
- Orden de magnitud: Cada dígito se multiplica por una potencia de la base según su posición.
- Cero como referencia: Algunos sistemas incluyen el número 0, mientras que otros no (como los romanos y egipcios).
- Conversión entre sistemas: Es posible transformar números de un sistema a otro.
Estas propiedades son esenciales para comprender la numeración y aplicarla en diferentes áreas del conocimiento.
